This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Yici Zhong, Department of Physics, Graduate School of Science, University of Tokyo, Bunkyo-ku, Tokyo 113-0033, Japan;
(2) Kazumi Kashiyama, Research Center for the Early Universe, Graduate School of Science, University of Tokyo, Bunkyo-ku, Tokyo 113-0033, Japan and Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU,WPI), The University of Tokyo, Chiba 277-8582, Japan;
(3) Shinsuke Takasao, Department of Earth and Space Science, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan;
(4) Toshikazu Shigeyama, Research Center for the Early Universe (RESCEU), School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan and Department of Astronomy, School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan;
(5) Kotaro Fujisawa, Research Center for the Early Universe (RESCEU), School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan and Department of Liberal Arts, Tokyo University of Technology, Ota-ku, Tokyo 144-0051, Japan.
Table of Links
Appendix
C. Change of the Mass Loss Rate in MHD Regime
3. RESULT
Table. 3 shows a summary of our simulation. A model BxΩy corresponds to the case with B∗ = x and Ω∗ = y in the cgs unit. When the rotating magnetic wind becomes quasi-steady, it can be characterized by the mass loss rate
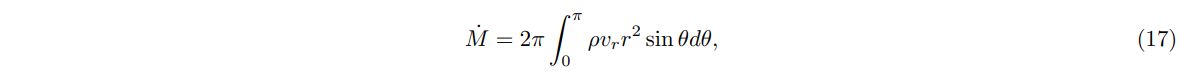
wind luminosity
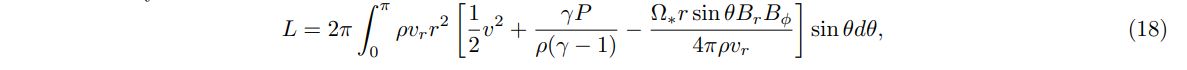
and spindown torque
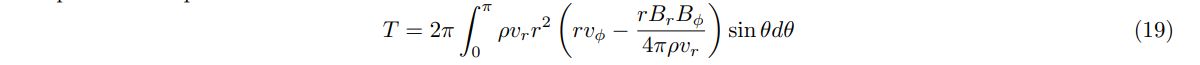
estimated at the outer boundary. As we show later, the strength of rotating magnetic winds can be characterized by
a dimensionless parameter
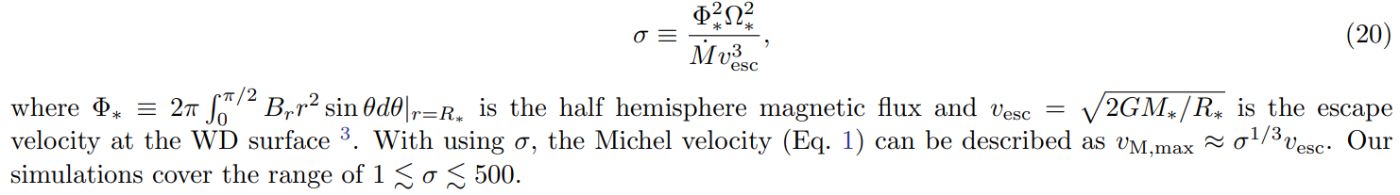
Hereafter we take B1.5e6Ω0.23 with σ = 34.3 as the fiducial model, and first show the multi-dimensional structure of the rotating magnetic wind in Sec. 3.1. We then investigate the time variability of the system primarily focusing on the impacts of quasi-periodic eruption along with the equatorial plane in Sec. 3.2. Finally, we show how the time-averaged spin-down torque scales with system parameters in Sec. 3.3.
3.1. Anisotropic wind structure


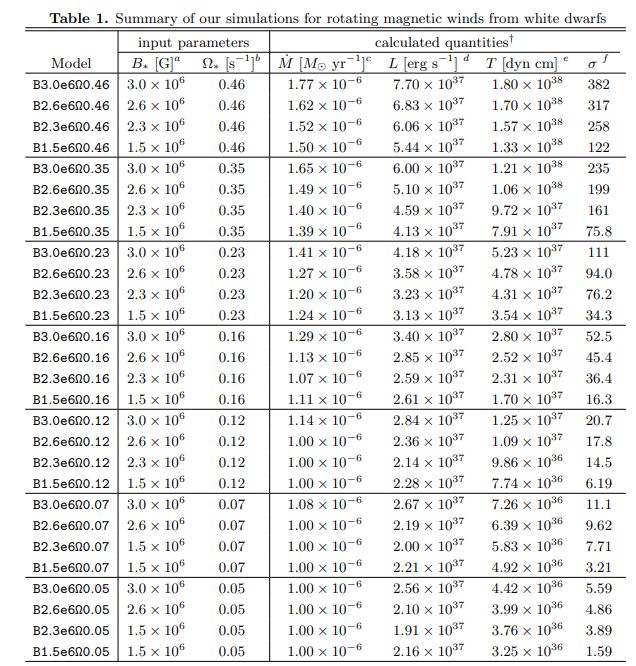
In the equatorial direction (80◦ ≲ θ ≲ 100◦), magnetic fields are closed at small radii, forming a corotating magnetosphere. Beyond the last closed loop, the magnetic field lines are open with a predominant toroidal component, having opposite polarities with respect to the equatorial plane. The transition of the magnetic field configuration is mediated by reconnection occurring at around the tip of the last closed loop, or the Y point. As can be observed from the top-right panel of Fig. 1, the plasma beta in this transition region is higher than those along the open magnetic fields, implying that the gas is trapped mainly by magnetic tensions. In this high plasma-beta region sandwiched by low plasma beta regions, gases are pinched and radially accelerated in the reconnection region, eventually become supersonic at around r ∼ 5 R∗.

The latitudinal angle dependence of the wind at the outer boundary is illustrated in Fig. 2, where the gray shaded regions represent the dynamical range of radial velocity (top-left), luminosity (top-right), torque (bottom-left), and mass loss rate (bottom-right). As described in the previous paragraphs, radial velocities in the near-equatorial direction can reach and transiently exceed the Michel velocity (represented by the horizontal dotted line) during eruptions caused by reconnection at the Y-point. Consequently, the wind luminosity, dominated by the radial kinetic term, also exhibits a sharp peak in the equatorial direction. On the other hand, the torque is primarily exerted by corotation with the magnetic fields and reaches its peak slightly off the equatorial plane (θ ∼ 85◦), corresponding to the edge of the concave shape of the Alfven radius.
3.2. Time variability
The acceleration of the rotating magnetic wind in the equatorial direction occurs in a time-variable manner, associated with magnetic reconnection at the Y-point. Consequently, the overall flux of mass, energy, and angular momentum from the central WD can also vary with time. Fig. 3 displays the time evolution of the mass loss rate (M˙ ), luminosity (L), and torque (T) in our fiducial model. All quantities are normalized by their time-averaged values.
The lower panel of Fig. 3, which provides a long-term perspective, reveals a recurrent eruptive behavior. A recurrent cycle consists of pre-eruption, reconnection, post-eruption phases: In the pre-eruption phase, gases injected into the near-equatorial plane become trapped within the closed field lines. Due to the centrifugal force, the gases accumulate at the tip of the last closed loop, resulting in a continuous decrease in plasma beta in that region. When the centrifugal force acting on the accumulated gases exceeds the tension of the closed magnetic fields, the tip of the closed zone starts expanding radially and is subsequently ejected as a plasmoid through reconnection. Such a plasmoid can be observed at r ∼ 4 - 5 R∗ in Fig. 1. Afterwards, the cycle returns to the pre-eruption phase and restores the gases within the closed magnetic field lines. This type of recurrent eruptions has been known as slingshot prominence in the context of magnetically-active rapidly-rotating stars (e.g., Ferreira 2000; Townsend & Owocki 2005; Jardine & Collier Cameron 2019).
The upper panel of Fig. 3 focuses on the fluxes during a rotation period (t = 15-16 [2π/Ω∗]), as also depicted in Fig. 2. In comparison to the pre- and post-eruption phases, represented by the purple and red lines, respectively, the observed fluxes of mass, energy, and angular momentum consistently increase as the erupted plasmoids reach the outer boundary, indicated by the green lines. Notably, the magnetic torque significantly contributes to the overall torque increase during the eruption phase and plays a dominant role in the central WD’s spin-down.
![Figure 2. Latitudinal angle dependence of the rotating magnetic wind of B1.5e6Ω0.23 showing the radial velocity vr (top leftpanel), the wind luminosity L (top right panel), the torque T (bottom left panel), and the mass loss rate M˙ (bottom right panel) at the outer boundary. A time sequence during a rotation period (t = 15-16 [2π/Ω∗]) is represented with colors across the gray shaded region, indicating the entire dynamic range during the simulation. The thick purple, green, and red lines highlight the timings of pre-eruption, eruption, and post-eruption, respectively. These timings are marked with vertical dashed lines in the upper panel of Fig. 3. The orange dotted line in the top left panel indicates the Michel velocity (Eq. 2).](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-rbj3uoj.jpeg)
We note that the specifics of reconnection dynamics, such as the frequency of recurrent eruptions and the resulting time evolution of mass, energy, and angular momentum fluxes, may be influenced by our numerical parameters, including spatial resolution (which governs numerical resistivity) and the width of the wind launching region. However, we have verified that the time-averaged values of wind velocities, mass loss rate, luminosity, and torque have all reached convergence concerning the spatial resolution in our simulations and the width of the wind launching region (see Appendix B).
3.3. Scaling relation of the spin-down torque
Here we consider how the spin-down torque of rotating magnetic wind depends on the system parameters based on our numerical results. As we show in the previous sub-sections, the time-averaged torque is essentially determined by the magnetic torque exerted on the gases at the tip of the last closed field lines, or the Y-point, where the field configuration is still roughly compatible with the rotating dipole. In this case, the (electro)magnetic torque at the Y point can be estimated as
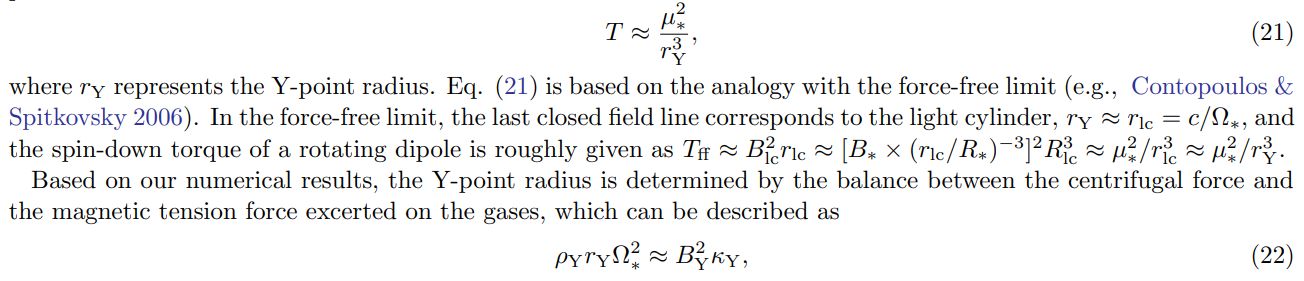
![Figure 3. Time evolution of mass loss rate M˙, luminosity L, and torque T of the rotating magnetic wind of B1.5e6Ω0.23estimated at the outer boundary of the computational domain. The quantities are normalized by the time-averaged values.
The upper panel displays a close-up view of a rotation period (t = 15-16 [2π/Ω∗]), where the vertical dashed lines indicate the timings of pre-eruption, eruption, and post-eruption highlighted in Fig. 2.](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-sim3uwl.jpeg)



[3] In relativistic MHD regime, speed of light c is conventionally used as the characteristic speed of the system (e.g., see the definition of σ0 in Bucciantini et al. 2006).
